Chapter 3 Discrete distributions
When we presented the axioms of probability in Chapter 2 we mentioned the concept of a sample space and probability. For the sake of brevity we will skip almost all of the set theoretic foundation of probability measures and will directly introduce the concept of a random variable.
Let us go back to the roots of probability theory that date back at least to the 17th century and the study of games of chance (gambling) (Freedman, Pisani, and Purves 2007, 248). Almost all introductory treatments of probability theory start with an example of some simple game of chance. We will follow this example, because it is easy to understand a simple game and the mathematical concepts involved. Later we will see how we can apply the concepts developed here to an extremely broad range of problems.
3.1 Discrete Random Variables
Imagine that you are about to buy a lottery ticket that costs 1 EUR. Until you buy and scratch the ticket you don’t actually know how much you will win, but before you commit to the purchase you may wonder what winnings you should expect. Without knowing the rules of the lottery you would be completely in the dark about your prospects, so let us assume that you actually how the lottery works. From our point of view the rules of the game are completely determined by two things. The first one is the set of possible outcomes (the sample space) of the lottery and let’s assume that each ticket can win 0 EUR, 1 EUR or 2 EUR. Notice that the set of possible values is finite as there are only three possible outcomes. Let us write \(X\) for the (yet unknown) win from our lottery ticket. In lottery games the value of \(X\) depends on some random mechanism (for example drawing numbered balls, spinning a wheel, etc.), therefore it is a function of the outcome of this random mechanism. We will call functions like \(X\) random variables. For the most part we will not refer the underlying random mechanism and will simply focus on the distribution of the possible values of \(X\). The second part of the rules is how often winnings of 0 EUR, 1 EUR and 2 EUR occur when you repeatedly play the game. Obviously, a game where half of the tickets win 2 EUR is quite different from a game where only one out of 100 tickets wins 2 EUR.
| Winnings (x) | \(p(x)\) | Winnings (y) | \(p_{y}(y)\) |
|---|---|---|---|
| 0 EUR | 0.5 | 0 EUR | 0.5 |
| 1 EUR | 0.3 | 1 EUR | 0.1 |
| 2 EUR | 0.2 | 2 EUR | 0.3 |
Let us focus on the first game with probabilities (0.5, 0.3 and 0.2) and develop some intuitive understanding of these quantities. You can think about the probabilities in Table 3.1 as theoretical proportions in a sense that if you play the lottery 100 times you would expect to win nothing (0 EUR) in about 50 games, 1 EUR in about 30 games and 2 EUR in about 20 games. Notice that to expect 20 2-EUR wins out of 100 games is absolutely not the same as the statement that you will win 2 EUR in exactly 20 out of 100 games! To convince yourself look at 3.2 which presents the results of five simulated games with 100 tickets each. You can play with this and similar games by changing the number of tickets and the number of games in this simulation. In the first game the player had 49 tickets that won nothing, but in the second game she had only 38 0-win tickets. When we say to expect 50 0-wins out of 100 tickets we mean that the number of observed (actually played) 0-wins will vary around 50. In neither of the five simulated games was the number of 0-wins exactly equal to 50 (this is also possible, though).
| x = 0 | x = 1 | x = 2 | average ticket win | |
|---|---|---|---|---|
| Game 1 | 49 | 34 | 17 | 0.68 |
| Game 2 | 38 | 36 | 26 | 0.88 |
| Game 3 | 47 | 31 | 22 | 0.75 |
| Game 4 | 49 | 26 | 25 | 0.76 |
| Game 5 | 62 | 23 | 15 | 0.53 |
The probabilities in 3.1 completely describe the game. The function that assigns a probability to each possible outcome \(p(x)\) is called a probability mass function. This function gives us everything there is to know about our hypothetical game. While this knowledge will not guarantee you a profit from gambling, it enables you to to compute the expected value of each ticket, the probability that none of your tickets will win, etc. An important property of the probability mass function is that it is always non-negative (no negative probabilities) and that the sum of the probabilities over all possible values is exactly \(1\).
\[\begin{align} P(X = x_k) = p(x_k). \end{align}\]
The probabilities must be non-negative and need to sum to 1 over all possible values. \[\begin{align} p(x_k) \geq 0\\ \sum_{k = 1} ^ {K} p(x_k) = 1. \end{align}\]
Note that the set of \(K\) possible values \(x_1,\ldots,x_K\) is finite. The same definition can be used for infinite sets of possible values as long as these are countably infinite but we will omit this discussion.
Closely related is the cumulative distribution function:
which gives the probability for events of the type \(X \leq x\).
\[\begin{align} P(X < 1) & = \sum_{x_k < 1} p(x_k) = p(x_1) = 0.5. \\ P(X \leq 1) & = \sum_{x_k \leq 1} p(x_k) = p(x_1) + p(x_2) = 0.5+ 0.3= 0.8\\ P(X < 2) & = \sum_{x_k < 2} p(x_k) = p(x_1) + p(x_2) = 0.5+ 0.3= 0.8\\ P(X \leq 2) & = \sum_{x_k \leq 2} p(x_k) = p(x_1) + p(x_2) + p(x_3) = 0.5+ 0.3+ 0.2= 1\\ \end{align}\]
3.2 Expected value
Just as the descriptive statistics (average, empirical median, empirical quantiles, etc.) are useful for summarising a set of numbers we would like to be able to summarise distribution functions.
Imagine that you plan to buy 100 tickets from the first game in Table 3.1. Based on the interpretation of probabilities as theoretical proportions you would expect that 50 of the tickets will win nothing, 30 of the tickets will bring you 1 EUR and 20 of the tickets will win 2 EUR. Thus you can write the expected winnings per ticket by summing the contributions of each ticket type:
\[\begin{align} \text{expected winnings} & = \underbrace{\frac{50}{100} \times 0\text{ EUR}}_{0\text{ EUR tickets}} + \underbrace{\frac{30}{100} \times 1\text{ EUR}}_{1\text{ EUR tickets}} + \underbrace{\frac{20}{100} \times 2\text{ EUR}}_{2\text{ EUR tickets}} \\ & = 0.5 \times 0 \text{EUR} + 0.3 \times 1 \text{EUR} + 0.2 \times 2 \text{EUR} = 0.7\text{EUR}. \tag{3.1} \end{align}\]
Note that the coefficients before the possible outcomes are simply their probabilities. Therefore in a game with 100 tickets you expect that each ticket will bring you \(0.7\) EUR (on average). Just as with the probabilities, the expected values does not tell you that your average win per ticket will be EUR. If you take a look at the five simulated games in Table 3.2 you will notice that the realised average ticket wins are not equal to but they vary around it. You can think about the expected value as the centre of the distribution (see Figure 3.1 and Freedman, Pisani, and Purves (2007), pp. 288). It is important to see that the expected value only depends on the probabilities and the possible values and it does not depend on the outcome of any particular game. Therefore it is a constant and not a random variable itself.
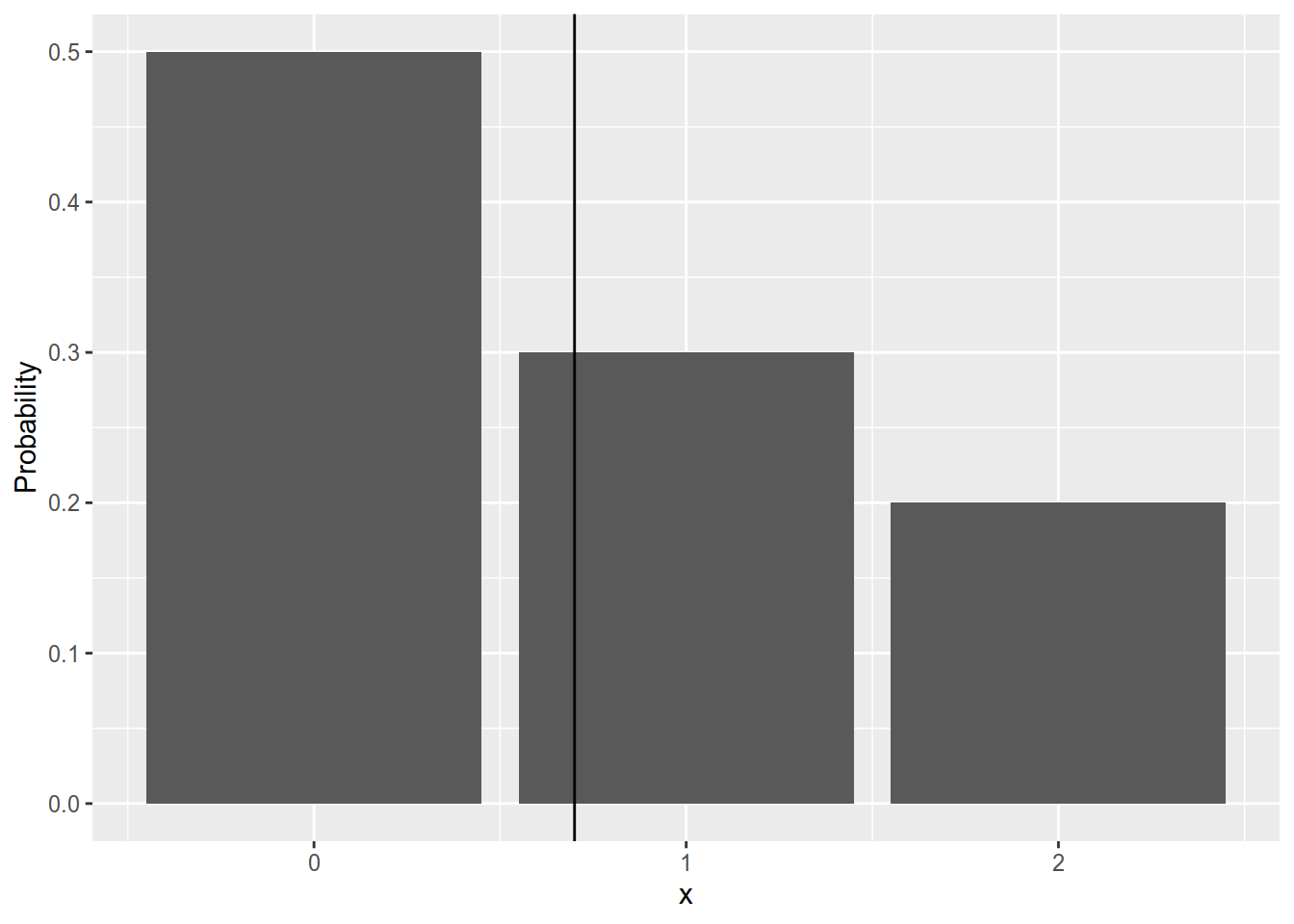
Figure 3.1: Probabilities plot. The black vertical line depicts the expected value.
Let us write the expected value in a more general way:
Definition 3.3 (Expected value) For discrite random variable \(X\) with possible values \(x_1, x_2,\ldots,x_n\) the weighted average of the possible outcomes: \[\begin{align} E(X) = \sum_{i = 1} ^ {n} x_i p(x_i) \tag{3.2} \end{align}\] is called the expected value of \(X\). Sometimes we will refer to the expected value as the mean of the distribution or the mean of the random variable following the distribution.
We introduced the expected value with an example of a game with 100 tickets in order to illustrate it. You should notice from 3.3 that the expected value is independent of the number of games played.
Exercise 3.1 Let \(Y\) be a game with possible outcomes 0, 1, and 2 EUR. The probabilities of these outcomes are given by \(p_1(x)\) in Table 3.1. Calculate the expected value of \(Y\).
\[\begin{align} E(Y) = \sum_{i = 1} ^ 3 p_{y,i} x_i = 0.5\times 0+ 0.3\times 1+ 0.2\times 2= 0.7. \tag{3.3} \end{align}\]3.2.1 Properties of the expected value
In the following we list a few important properties of the expected value that we will use throughout the course. In the following let \(X\) and \(Y\) be random variables with expected values \(E(X)\) and \(E(Y)\).
\[\begin{align} E(X + Y) = E(X) + E(Y) \tag{3.4} \end{align}\]
\[\begin{align} E(a) = a. \tag{3.5} \end{align}\]
\[\begin{align} E(aX) = aE(X). \tag{3.6} \end{align}\]
3.3 Variance
Let us compare the two games in Table 3.1. Both have the same sample space (set of possible outcomes) and both have the same expected winnings, see (3.1) and (3.3). The games are not identical, though, because their probability distributions are different. If given the choice to play only one game, which one would you prefer?
The second game offers a higher probability to win the highest prize (EUR) at the cost of a lower probability for the middle prize (EUR). In other words it places a higher probability on extreme outcomes (outcomes that are far from the centre of the distribution, i.e. the expected value). A summary of a distribution that measures its spread (i.e. how likely are extreme values) is the variance:
Definition 3.4 (Variance) For a discrete random variable \(X\) with possible outcomes \(x_1, x_2,\ldots,x_n\) and probability function p(x) the variance is the expected quadratic deviation from the expected value of the distribution \(E(X)\).
\[\begin{align} Var(X) & = E(X - E(X)) ^ 2 \\ & = \sum_{i = 1} ^ n \left(x_i - E(X)\right) ^ 2 p(x_i) \end{align}\]
Example 3.2 The variance of the first game (X) is: \[\begin{align} Var(X) & = \sum_{i = 1} ^ {3} (x_i - E(X)) ^ 2 p(x_i) \\ & = (x_1 - E(X)) ^ 2 p(x_i) + (x_2 - E(X)) ^ 2 p(x_2) + (x_3 - E(X)) ^ 2 p(x_3) \\ & = (-0.70) ^ 2 \times 0.5+ (0.30) ^ 2 \times 0.3+ (1.30) ^ 2 \times 0.2\\ & = 0.61. \end{align}\]
Exercise 3.2 Compute the variance of \(Y\), the second game described in Table 3.1.
Solution. \(Var(Y) = 0.76\).
\[\begin{align} P(X = x_k, Y = y_l) = P(X = x_k)P(Y = y_l) \end{align}\]
Theorem 3.4 (Variance of the sum of independent random variables) For two independent random variables \(X\) and \(Y\). We will introduce the concept of independence later.
\[\begin{align} Var(X + Y) = Var(X) + Var(Y) \tag{3.7} \end{align}\]
Theorem 3.4 actually holds even for uncorrelated variables. We will discuss the concept correlation later.
Another useful formula for working with the variance is:\[\begin{align} Var(aX) = a^2 Var(X) \tag{3.8} \end{align}\]
Proof. \[\begin{align} Var(aX) & = \sum_{k = 1} ^ K (ax_k - E(aX))^2 p(x_k) \\ & = \sum_{k = 1} ^ K a^2(x_k - E(X))^2 p(x_k) \\ & = a^2 \sum_{k = 1} ^ K a^2(x_k - E(X))^2 p(x_k) \\ & = a^2 Var(X). \end{align}\]
Often it will be easier to compute the variance using the following decomposition: \[\begin{align} Var(X) & = E(X - E(X))^2 \\ & = E\left(X^2 - 2XE(X) + E(X) ^ 2\right) \\ & = E(X^2) - E(2XE(X)) + E(E(X) ^ 2) \\ & = E(X^2) - 2 E(X)E(X) + E(X) ^ 2 \\ & = E(X^2) - E(X)^2 \tag{3.9}. \end{align}\] The proof above uses the fact that \(E(X)\) is a constant and applies Theorems 3.2 and 3.3.
References
Freedman, David, Robert Pisani, and Roger Purves. 2007. Statistics. W W NORTON & CO. https://www.ebook.de/de/product/6481761/david_freedman_robert_pisani_roger_purves_statistics.html.