Chapter 8 Linear regression
This chapter presents the core material of the introductory econometrics course and provides detailed explanations to the solutions of the assignments in Chapter 9.
8.1 Intercept only model
8.1.1 The model
Consider the example discussed in Section 9.2. There we discuss data on \(n = 114\) covid-19 patients with known incubation times \(y_1, y_2, \ldots, y_n\).
Before we begin with the discussion of the model presented in that assignment let us first summarise the data.
| Min. | 1st Qu. | Median | Mean | 3rd Qu. | Max. |
|---|---|---|---|---|---|
| 1.5 | 3 | 4 | 5.394737 | 6 | 24.5 |
The average incubation time was 5.39 days. The shortest incubation period was 1.50 days and the longest one was 24.50 days. Half of the patients developed symptoms after less than 4.00 days.
You will notice that the incubation times differ from person to person. We are not going to answer the question why these times are different. Instead, we are going to attempt to describe this variation with a simple model.
Consider a deterministic model for the incubation times:
\[\begin{align} y_i = \beta_0, \quad, i = 1,\ldots,n. \tag{8.1} \end{align}\]
which implies that the incubation time is one and the same and equal to \(\beta_0\) for all patients, e.g. \(\beta_0 = 5\) days. A glance at Table 8.1 and Figure 8.1 should convince us that (8.1) cannot hold as the observed times differ between patients. If all incubation times were equal all points in Figure 8.1 would lie on a single straight line.
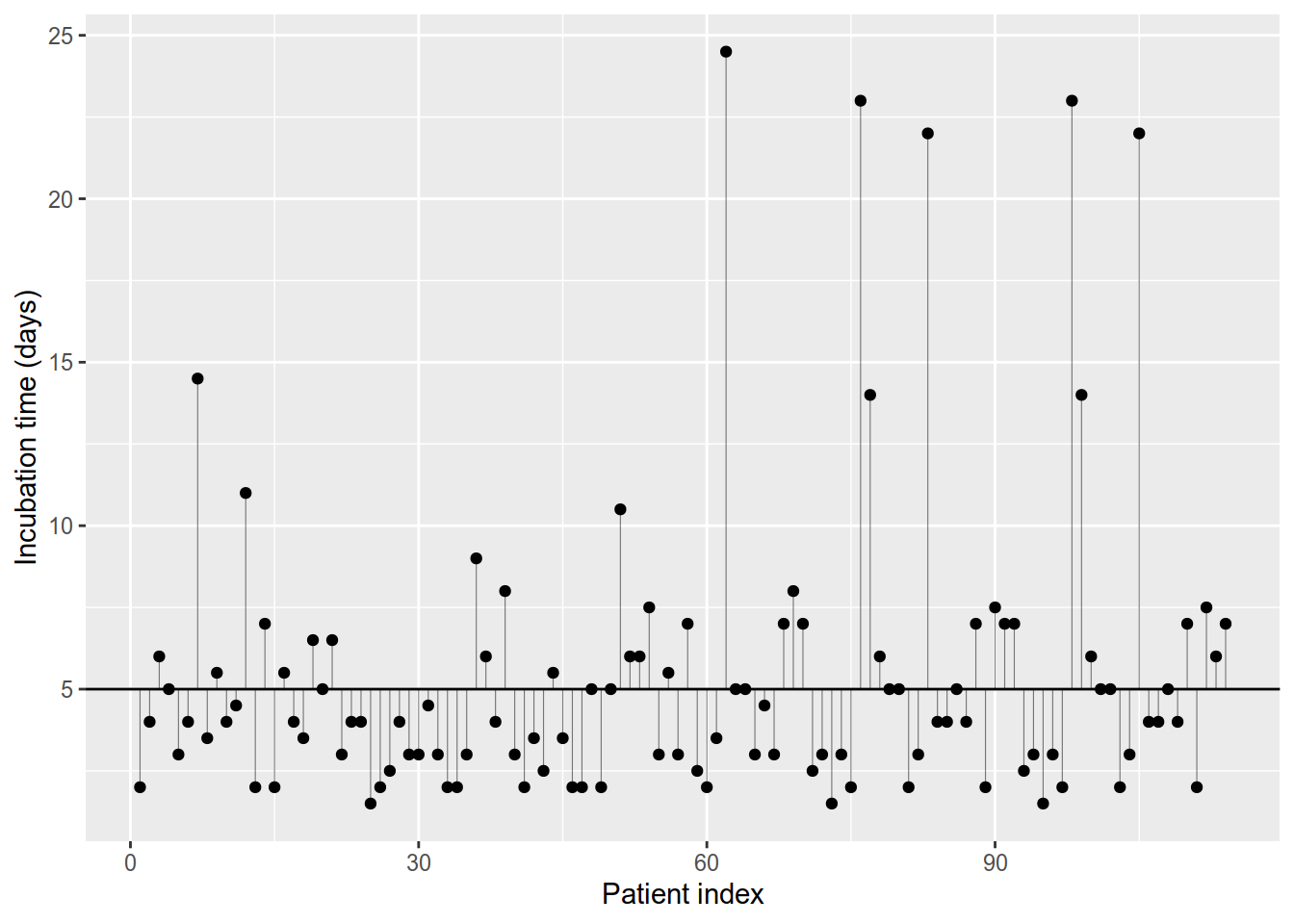
Figure 8.1: Incubation times plot. The thin vertical lines depict the differences between observed times (points) and 5 days (horizontal line).
We can relax the assumption in (8.1) by adding the difference between the observed \(y_i\) and \(\beta_0\): \(u_i = y_i - \beta_0\).
\[\begin{align} y_i = \beta_0 + u_i. \tag{8.2} \end{align}\]
Our second approach would describe the observed incubation times perfectly but that trick has achieved little other than adding more mathematical notation. Model (8.2) has more parameters than there are data points (observations): \(n\) deviations and \(\beta_0\). Furthermore we cannot use (8.2) to predict the incubation time of persons whom we have not seen yet, because we need to know their incubation time in order to compute \(u\) and this defeats the purpose of a prediction.
Let us look at another approach. Instead of computing the individual deviations \(u_i\) for each person let us views the deviation for person \(i\) as a realisation of a random variable \(u_i\). When we say a random variable we need to describe its distribution at the very least by assuming something about the expected values and the variances of \(u_1,\ldots,u_n\). For now we will assume that all \(u_i\) terms have a common expected value of zero and variance \(\sigma ^ 2\) that does not depend on the individual patient. We will even go further and assume that the \(u_i\) are independent and normally distributed. In this way we can describe the deviations with a single parameter \(\sigma ^ 2\).
Note that these are all assumptions that we need to question and we will address this in later chapters. For now we will examine the implications of the assumptions.
Our model is now: \[\begin{align} y_i = \beta_0 + u_i, \quad i=1,\ldots,n \tag{8.3} \end{align}\]
where the errors terms \(u_1,u_2,\ldots,u_n\) are independent, identically distributed (iid) random variables with zero mean and variance \(\sigma ^ 2\), i.e. \(N(0, \sigma ^ 2)\).
Using Theorems 3.1, 3.2 and 3.4 we see that the expected value of \(y_i\) is \(\beta_0\) and that its variance is \(\sigma ^ 2\). We are also using that \(\beta_0\) is a unknown but fixed value (a real number) and is not random.
\[\begin{align} E(y) & = E(\beta_0 + u) \\ & = E(\beta_0) + E(u) \\ & = \beta_0 + 0 \\ & = \beta_0 \end{align}\] \[\begin{align} Var(y) & = Var(\beta_0 + u) \\ & = Var(\beta_0) + Var(u) \\ & = 0 + \sigma ^ 2 \\ & = \sigma ^ 2 \end{align}\]
\(y_i\) is thus normally distributed with expected value \(\beta_0\) and variance \(\sigma^2\). \[\begin{align} y \sim N(\beta_0, \sigma ^ 2). \tag{8.4} \end{align}\]
The coefficient \(\beta_0\) is simply the expected incubation time.
It is important to know what model (8.4) does not imply. It doesn’t say that the incubation times are constant. So to say that the incubation time is 8 days does not make much sense without a reference to an observed patient. Saying that the incubation time of patient 1 was 2 days is OK (this is an observed value). Saying that the expected incubation time is \(\beta_0 = 8\) is also OK.
Model (8.4) states that the incubation time is a random variable. This means that we cannot know the exact incubation time for a new patient. We are not completely in the dark, though, because equation (8.4) tells us something about the structure of the randomness. Assuming this model is true and we know its parameters to be \(\beta_0 = 5, \sigma ^ 2 = 4 ^ 2\) (for example) then some incubation periods are more likely than others. Let us compute the probability for an incubation period that is longer than 30 days under model (8.4).
## [1] 2.052264e-10\[\begin{align} P_{N(5, 4 ^ 2)}(Y > 30) = 1 - P_{N(5, 4 ^ 2)}(Y < 30) = 2.0522639\times 10^{-10} \end{align}\]
The probability of an incubation period of less than 2 days is (under the model):
## [1] 0.2266274\[\begin{align} P_{N(5, 4 ^ 2)}(Y < 2) = 0.2266 \end{align}\]
8.1.2 The prediction
Let us for now pretend that we actually know the expected incubation time (let it be equal to \(\beta_0 = 5\)) and that the incubation times are normally distributed as per model (8.3). How would we predict the incubation time for new (yet unseen) patients? If our prediction is one and the same number of days for all patients, then what is the best prediction? Is it 4, is it 5, 6, 9 days? If we are asking about what is the best prediction then we must define what a good prediction is and what a bad prediction is. There are multiple ways to do this but here we will examine only one.
Let \(Y\) be the incubation period of the new patient and let \(\hat{y}\) be our prediction for that period. Until we wait and see when that patient starts to show symptoms we don’t know the actual value of \(Y\). While we don’t know what value \(Y\) will turn out to have (it is random) we can still think about the error of our prediction. The error of our prediction will be \(\hat{y} - Y\), whatever \(Y\) turns out to be. If our prediction is 2 days and the actual incubation period turns out to be 5 days, then the error will be \(2 - 5 = -3\) days. We would have underestimated the incubation period of that patient by 3 days. If the incubation period turns out to be one day and we predict it to be 2 days, then we would have overestimated it by 1 day (\(1 - 2 = -2\)).
Because \(Y\) is random, we must give up any hope to predict the incubation period perfectly. What we can do is find the prediction that makes our errors “small” in some sense. Be aware that every time that we mention “small”, “large”, etc, we need to say what exactly is small and what exactly is large.
When we make predictions we must know that wrong predictions have consequences. Imagine again the patient whose actual incubation time was 5 days and we predicted it to be 3 days. After the third day she may think that the incubation period is over (it is not over) and may stop observing a quarantine, potentially infecting other people over the course of two whole days.
As we see that prediction errors entail consequences we should be careful and we must attempt to make these as small as possible. Let us denote the error to be:
\[\begin{align} Y - \hat{y}. \end{align}\]
and imagine that we incur a penalty for each deviation between \(Y\) and \(\hat{y}\) in a way so that we lose
\[\begin{align} Loss(\hat{y}) = (Y - \hat{y}) ^ 2 \tag{8.5} \end{align}\]
for each prediction. We would like to avoid large penalties and we may attempt to minimise the expected loss form wrong predictions by choosing \(\hat{y}\) so that (8.5) is as small as possible. Remember that the average loss over a large number of predictions will be close to the expected loss.
\[\begin{align} E(Loss(\hat{y})) = E(Y - \hat{y})^2 \tag{8.6} \end{align}\]
Expanding the right-hand side of (8.6) gives:
\[\begin{align} E(Loss(\hat{y})) & = E(Y - \hat{y})^2 \\ & = E(Y ^ 2 - 2Y\hat{y} + \hat{y} ^ 2) \\ & = E(Y ^ 2) - 2\hat{y}E(Y) + \hat{y} ^ 2. \tag{8.7} \end{align}\]
Notice that (8.5) and therefore (8.7) don’t involve random quantities, because the expected value of a random variable is a fixed number and is not random (see for example ??). Furthermore, \(E(Y)\) and \(E(Y ^ 2)\) do not depend on \(\hat{y}\) (this would mean that our prediction changes the distribution of incubation times). To find the minimum of (8.7) we can differentiate with respect to \(\hat{y}\) and set the derivative to zero:
\[\begin{align} \frac{\partial E(Loss(\hat{y}))}{\partial \hat{y}} & = 0 - 2E(Y) + 2\hat{y} = 0 \\ \implies \hat{y} = E(Y). \end{align}\] The second derivative of (8.7) with respect to \(\hat{y}\) is 2 and is positive, therefore the expected loss has a minimum at \(\hat{y} = E(Y)\).
To summarise, predicting the incubation time using \(E(Y)\) minimises the expected square loss from prediction errors.
8.1.3 OLS estimator
By now we have established how to predict incubation times using \(E(Y)\) but we have (rather unrealistically) assumed that we know parameter \(\beta_0\) in (8.4). If this was in fact the case we could skip everything else in this chapter. In many situations this parameter is not known and we need to “guess” or “learn” it from observed data (the sample).
Once we have some “guess” \(\hat{\beta}_0\) about \(\beta_0\) we can use it to predict the incubation time of yet unseen patients. The estimated regression equation is: \[\begin{align} \hat{y} = \hat{\beta_0}. \tag{8.8} \end{align}\]
Let us now turn to the question how to generate a “good” guess for \(\beta_0\) from the data. Let us denote the predicted value for the \(i\)-th observation \(y_i\) with with \(\hat{y}_i\). Let us pick, rather arbitrarily, a value for \(\hat{\beta}_0\), say \(\hat{\beta}_0 = 8\). With this value we are able to use the model to predict the incubation time for yet unseen patients:
\[\begin{align} \hat{y} = 8. \end{align}\]
Are these predictions good? To answer this question we need to be able to say what is a good prediction and what is a bad prediction. We can evaluate the quality of our predicted incubation times \(\hat{y}_1,\ldots,\hat{y}_n\) when we compare these to the actually observed incubation times \(y_1, \ldots,y_n\). Loosely speaking predictions (model) that are far away from the observed values (reality) will be of little use. This might lead us to the idea to base our “guess” for \(\beta_0\) on the data in such a way so that the predicted values of the model (predictions) are as close as possible to the observed values (reality). In other words, the estimator for \(\beta_0\) must minimise the “distance” between the model (predictions) and the reality (observations). Since we have involved the notion of distance, we need to give it a more precise mathematical meaning in order to be able to minimise it. Consider the difference between an observed and a predicted value for some observation \(i\).
\[\begin{align} r_i = y_i - \hat{y}_i \tag{8.9} \end{align}\]
This value is called the residual of observation \(i\). For a good model the residuals \(r_i, i = 1,\ldots,n\) should be “small”. The ordinary least squares method (OLS) minimises the sum of squared residuals over all observations. Note that the residual \(r_i\) is not the same as the error term \(u_i\), hence the different names and the different symbols! The error terms are generally unobserved because \(\beta_0\) is unknown!
\[\begin{align} RSS = \sum_{i = 0} ^ n (y_i - \hat{y}_i) ^ 2. \tag{8.10} \end{align}\]
Because the predicted values \(\hat{y}_i\) depend on \(\hat{\beta}_0\), so does the residual sum of squares.
\[\begin{align} RSS(\hat{\beta_0}) = \sum_{i = 0} ^ n (y_i - \hat{y}_i) ^ 2 \tag{8.11}. \end{align}\]
Before we continue let’s make sure that you understand how to calculate the residual sum of squares given a concrete value of \(\hat{\beta}_0\).
\[\begin{align} RSS(5) & = (2.00 - 5) ^ 2 + (4.00 - 5) ^ 2 + (6.00 - 5) ^ 2 \\ & = 9.00 + 1.00 + 1.00 \\ & = 11.00. \end{align}\]
## [1] 2341\[\begin{align} RSS(3) = 46.25. \end{align}\]
Let us see now how RSS changes for different values for \(\hat{\beta}_0\). Figure 8.2 shows the value of RSS calculated for a range of values of \(\hat{\beta}_0\) between 0 and 11. You should notice the parabolic shape of curve (not surprising, since RSS involves squares) and that the RSS has a minimum near \(\hat{\beta}_0 \approx 5\).
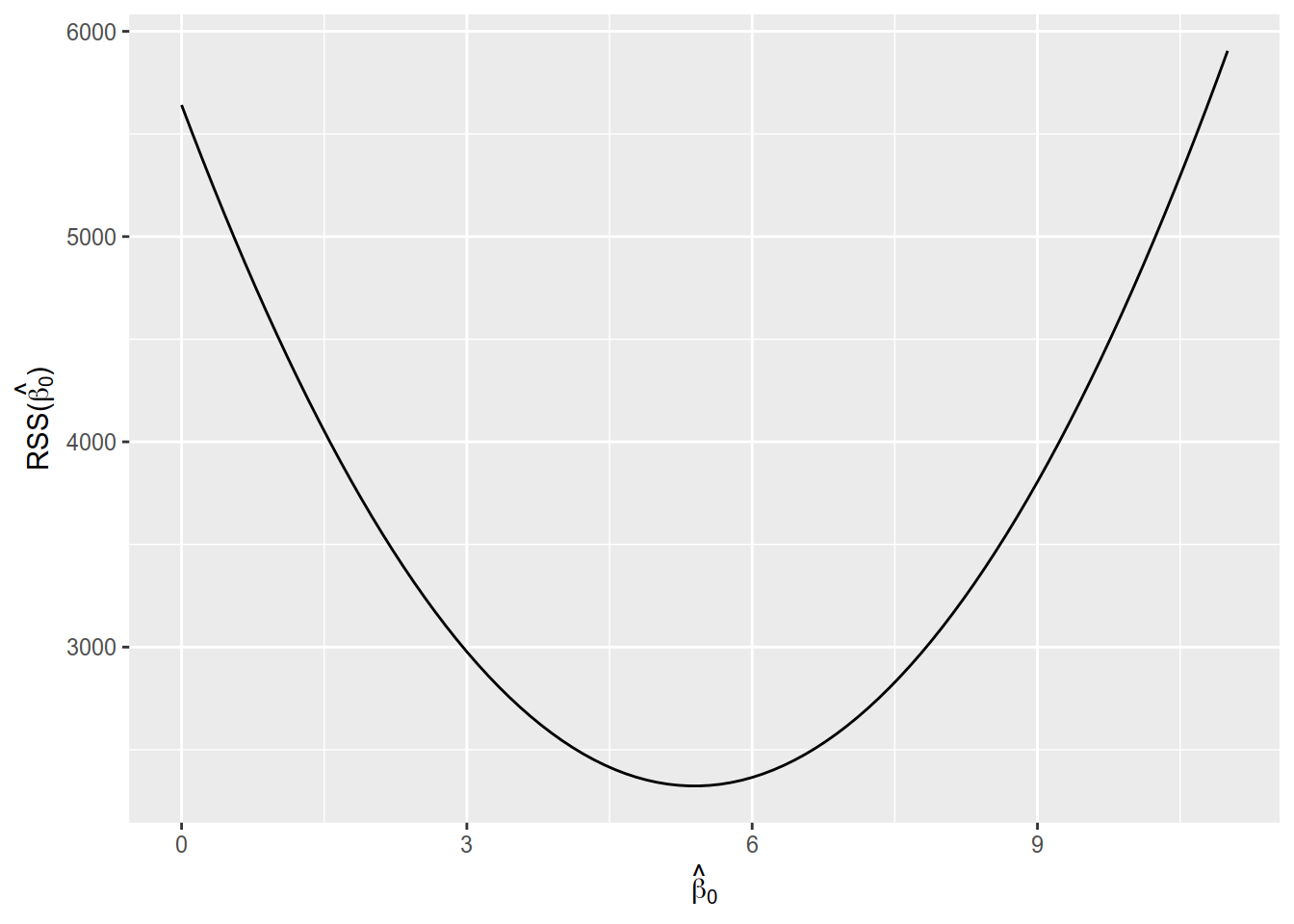
Figure 8.2: Residual sum of squares for values of \(\hat{\beta}_0\) between 0 and 11.
Can we find this minimum analytically using the tools we already know? To find the value of \(\hat{\beta}_0\) at the minimum we will differentiate RSS with respect to \(\hat{\beta}_0\) and will set the derivative to 0. Before we do that we will simplify (8.11) a little bit by expanding the parentheses and replacing \(\hat{y}\) with \(\hat{\beta}_0\) (because of (8.8)).
\[\begin{align} RSS(\hat{\beta_0}) & = \sum_{i = 0} ^ n (y_i - \hat{y}_i) ^ 2 \\ & = \sum_{i = 0} ^ {n}(y_i^2 - 2y_i\hat{y}_i + \hat{y}_i^2) \\ & = \sum_{i = 0} ^ {n}y_i^2 - 2 \sum_{i = 0} ^ n y_i\hat{y}_i + \sum_{i=0}^n \hat{y}_i^2 \\ & = \sum_{i = 0} ^ {n}y_i^2 - 2 \sum_{i = 0} ^ n y_i\hat{\beta}_0 + \sum_{i=0}^n \hat{\beta}_0^2 \\ & = \sum_{i = 0} ^ {n}y_i^2 - 2 \hat{\beta}_0\sum_{i = 0} ^ n y_i + n \hat{\beta}_0^2 \\ & = \frac{n}{n}\sum_{i = 0} ^ {n}y_i^2 - 2 \hat{\beta}_0\frac{n}{n}\sum_{i = 0} ^ n y_i + n \hat{\beta}_0^2 \\ & = n\overline{y^2} - 2 \hat{\beta}_0 n\bar{y} + n \hat{\beta}_0^2 \tag{8.12}. \end{align}\]
Let us find its first derivative with respect to \(\hat{\beta}_0\). The first term in the sum in (8.12), \(\overline{y^2}\), is simply \(n\) times the average of the squared values of \(y\) and it does not depend on \(\hat{\beta}_0\). The average of \(y\) in the second term in the sum (\(\bar{y}\)) also does not depend on \(\hat{\beta}_0\). Therefore we can treat both \(\bar{y^2}\) and \(\bar{y}\) as constants when we differentiate with respect to \(\hat{\beta}_0\) (i.e. their derivatives are zero).
\[\begin{align} \frac{\partial RSS(\hat{\beta}_0)}{\partial \hat{\beta}_0} = 0 - 2n\bar{y} + 2n\hat{\beta}_0. \tag{8.13} \end{align}\]
To find the extreme values of \(RSS(\hat{\beta}_0)\) we set the derivative in (8.13) to zero and solve the equation.
\[\begin{align} \frac{\partial RSS(\hat{\beta}_0)}{\partial \hat{\beta}_0} & = - 2n\bar{y} + 2n\hat{\beta}_0 = 0 \\ \implies \hat{\beta}_0 = \bar{y}. \end{align}\]
The second derivative of \(RSS(\hat{\beta}_0)\) with respect to \(\hat{\beta}_0\) is
\[\begin{align} \frac{\partial^2 RSS(\hat{\beta}_0)}{\delta \hat{\beta}_0 ^2} & = 2n > 0. \end{align}\]
As the second derivative is positive, \(RSS(\hat{\beta}_0)\) has a minimum at \(\hat{\beta}_0 = \bar{y}\).
We will use the lm function to estimate linear regression models in R. The first argument of the function is a formula, a special object that is used to describe models. We specify our response variable (\(y\)) on the left hand side of the formula. On the right hand side we specify the predictor variables. In our simple case there are no predictor variables, so we instruct it to fit an intercept only model by writing 1. The data argument instructs the function where to evaluate variable names. In our case Incubation is a column in the table linton.
##
## Call:
## lm(formula = Incubation ~ 1, data = linton)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.8947 -2.3947 -1.3947 0.6053 19.1053
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.3947 0.4247 12.7 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.534 on 113 degrees of freedomYou can find \(\hat{\beta}_0\) in the Coefficients part of the fit summary under the row named (Intercept). For our data this is \(\hat{\beta}_0 = 5.39\).
Inserting the estimate for \(\beta_0\) (look at the regression summary) into (8.8) we obtain \[\begin{align} \hat{y} = 5.39. \end{align}\]
Our prediction of the incubation time of all patients will be \(5.39\), the estimated expected value. To confirm our analysis so far, you should compare the estimate for \(\beta_0\) with the sample mean and see that both are equal.
## [1] 5.3947378.1.4 Variance estimation
The second parameter in model (9.1) is the variance of the error term \(u\): \(\sigma ^ 2\).
We can estimate it using the sample variance of \(y\): \[\begin{align} S(y) = \frac{1}{n - 1} \sum_{i = 1}^n (y_i - \bar{y}) ^ 2. \tag{5.5} \end{align}\]
Take care to remember the difference between the variance of \(u\) which is a parameter of the distributions of \(u\) and \(y\), as we see from (8.4). The sample variance is a function of the data (\(y_1, y_2,\ldots,y_n\)) used to estimate \(\sigma ^ 2\). The value of the sample variance changes when the data changes. \(\sigma ^ 2\) does not change with the data!
Note that the residual sum of squares (8.10) reduces to \(n - 1\) times the sample variance, because \(\hat{y}_i = \hat{\beta}_0 = \bar{y}\) for each \(i=1,\ldots,n\):
\[\begin{align} RSS & = \sum_{i = 1}^n (y_i - \hat{y}_i) ^ 2 \\ & = \sum_{i = 1}^n (y_i - \bar{y}) ^ 2 \\ & = (n - 1) S(y). \end{align}\]
8.1.5 Hypothesis testing
In the previous parts we have derived the sample mean as the OLS estimator for the intercept in the intercept only model. In Chapter @ref(#hypothesis-tests) we showed how to perform t-test about the mean of a normal distribution and you can apply all the knowledge from there. Instead of repeating all the theory discussed there we will learn how to use the regression output of lm to conduct simple tests.
Let us look again at that output:
##
## Call:
## lm(formula = Incubation ~ 1, data = linton)
##
## Residuals:
## Min 1Q Median 3Q Max
## -3.8947 -2.3947 -1.3947 0.6053 19.1053
##
## Coefficients:
## Estimate Std. Error t value Pr(>|t|)
## (Intercept) 5.3947 0.4247 12.7 <2e-16 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## Residual standard error: 4.534 on 113 degrees of freedomThe ingredients of the test statistic were the sample mean \(\bar{X}\), the standard deviation of the sample, the sample size \(n\) and the expected value under the null hypothesis (\(\mu_0\)). For a two-sided alternative
\[\begin{align} H_0: \mu = \mu_0 \end{align}\]
we used the test statistic
\[\begin{align} T = \frac{\bar{X} - \mu_0}{S(X) / \sqrt{n}}. \end{align}\]
Let us rewrite it in the notation of the regression model. In our model the expected value of \(y\) is \(\beta_0\), the sample mean is \(\hat{\beta}_0\). For the value of \(\beta_0\) under the null hypothesis we will write \(\beta_0^{(0)}\). When you compare the denominator in the test statistic to the result for the variance of the sample mean in (5.4) you should see that the term in the denominator is simply the square root of the variance of the sample mean or in other words: it is the standard deviation of the sample mean. We call the standard deviation of an estimator its standard error and we will write \(SE(\hat{\beta}_0)\). With this additional notation the null hypothesis and the t statistic looks like:
\[\begin{align} H_0: \mu = \mu_0 \implies \beta_0 = \beta_0^{(0)} \end{align}\]
\[\begin{align} T = \frac{\hat{\beta}_0 - \beta_0^{(0)}}{SE(\hat{\beta}_0)}. \end{align}\]
Note that we have only rewritten the test statistic in terms of \(\hat{\beta}_0\) without changing anything at all, so all results from Chapter @ref(#hypothesis-tests) apply without changes, except that instead of \(X\) we use \(Y\) to denote the sample data.
8.1.6 Assumptions
To be continued…